Saturs

• Soļi
• Padoms

Ja esat matemātiķis vai grafisks programmētājs, jums, iespējams, būs jāatrod leņķis starp diviem dotajiem vektoriem. Šajā rakstā wikiHow parāda, kā tieši to izdarīt.

Soļi

1. daļa no 2: atrodiet leņķi starp diviem vektoriem

1. 

   Vektoru definīcija. Pierakstiet visu informāciju par diviem jūsu rīcībā esošajiem vektoriem. Pieņemsim, ka jums ir tikai norādītie to izmēru koordinātu parametri (saukti arī par komponentiem). Ja jūs jau zināt vektora garumu (lielumu), varat izlaist dažas no tālāk norādītajām darbībām.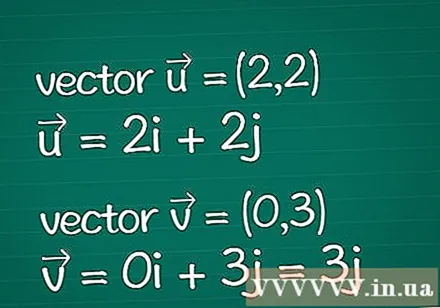
   • Piemērs: Divdimensiju vektors = (2,2) un divdimensiju vektors = (0,3). Tos var rakstīt arī kā = 2i + 2j un = 0i + 3j = 3j.
   • Lai gan šī raksta piemērā tiek izmantoti divdimensiju vektori, tālāk minētās instrukcijas var attiekties uz vektoriem ar jebkuru izmēru skaitu.

2. 

   
   
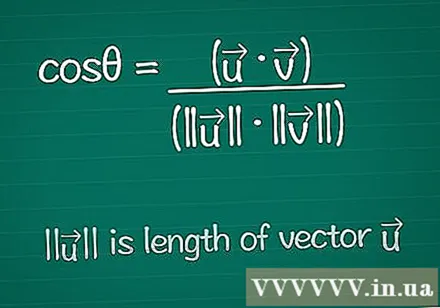
   Pierakstiet kosinusa formulu. Lai atrastu leņķi θ starp diviem vektoriem, mēs sākam ar formulu kosinusa atrašanai šim leņķim. Par šo formulu varat uzzināt tālāk vai vienkārši pierakstīt šādi:
   • cosθ = (•) / (|||| ||||)
   • |||| nozīmē "vektora garums".
   • • ir divu vektoru skalārais reizinājums - tas tiks paskaidrots turpmāk.

3. 

   
   
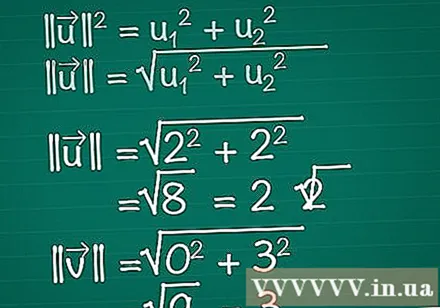
   Aprēķiniet katra vektora garumu. Iedomājieties, ka taisnstūra trīsstūri veido vektora x, y komponenti un pats vektors. Vektors veido trīsstūra hipotenūzu, tāpēc, lai atrastu tā garumu, mēs izmantojam Pitagora teorēmu. Faktiski šo formulu var viegli attiecināt uz vektoru ar jebkuru dimensiju skaitu.
   • || u || = u₁ + u₂. Ja vektoram ir vairāk nekā divi elementi, jums vienkārši jāturpina pievienot + u₃ + u₄ +...
   • Tādējādi divdimensiju vektoram || u || = √ (u₁ + u₂).
   • Šajā piemērā |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
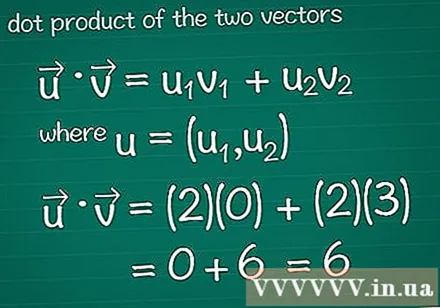
   Aprēķiniet divu vektoru skalāro reizinājumu. Varbūt jūs iemācījāties vektoru reizināšanas metodi, kas pazīstama arī kā skalārs šo. Lai aprēķinātu skalāro produktu, kas saistīts ar to sastāvu, reiziniet sastāvdaļas katrā virzienā kopā, pēc tam summējiet visu rezultātu.
   • Lūdzu, skatiet grafikas programmu, pirms lasāt tālāk.
   • Matemātikā • = u₁v₁ + u₂v₂, kur, u = (u₁, u₂). Ja vektoram ir vairāk nekā divi elementi, vienkārši pievienojiet + u₃v₃ + u₄v₄...
   • Šajā piemērā • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Tas ir vektora un vektora skalārais reizinājums.

5. 

   Ielieciet rezultātus formulā. Atcerieties, ka cosθ = (•) / (|||| || ||). Tagad mēs zinām gan skalāro reizinājumu, gan katra vektora garumu. Ievadiet tos formulā, lai aprēķinātu leņķa kosinusu.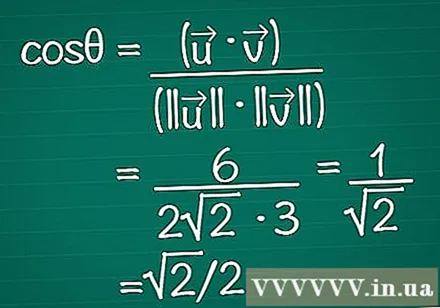
   • Mūsu piemērā cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Atrodiet leņķi, pamatojoties uz tā kosinusu. Varat izmantot arccos vai cos funkciju kalkulatorā, lai atrastu θ no zināmas cos vērtības. Izmantojot dažus rezultātus, jūs varat atrast leņķi, pamatojoties uz vienības apli.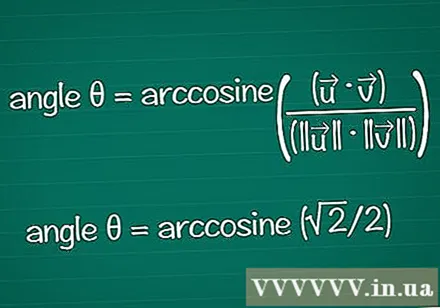
   • Piemērā cosθ = √2 / 2. Kalkulatorā ievadiet “arccos (√2 ​​/ 2)”, lai atrastu leņķi. Vai arī jūs varat atrast leņķi θ uz vienības apļa, pozīcijā cosθ = √2 / 2. Tas attiecas uz θ = /₄ vai 45º.
   • Apvienojot visu, galīgā formula ir: leņķis θ = arkozīns ((•) / (|||| || ||))
   reklāma

2. daļa no 2: Leņķa formulas noteikšana

1. 

   Izprotiet formulas mērķi. Šī formula nav atvasināta no esošajiem noteikumiem. Tā vietā tas tiek veidots kā skalārā produkta definīcija un leņķis starp abiem vektoriem. Pat tā tas nebija patvaļīgs lēmums. Atgriežoties pie pamata ģeometrijas, mēs varam saprast, kāpēc šī formula sniedz intuitīvas un noderīgas definīcijas.
   • Tālāk sniegtajos piemēros tiek izmantoti divdimensiju vektori, jo tos ir visvieglāk saprast un vienkāršāk. Trīsdimensiju vai vairākiem vektoriem ir īpašības, kuras nosaka gandrīz līdzīgas vispārīgās formulas.

2. 

   Pārskatiet Kosinusa teorēmu. Apsveriet parastu trijstūri ar leņķi θ starp malām a un b, pretējā pusē c. Kosinusa teorēma nosaka, ka c = a + b -2abcos(θ). Šis rezultāts tiek iegūts vienkārši no pamata ģeometrijas.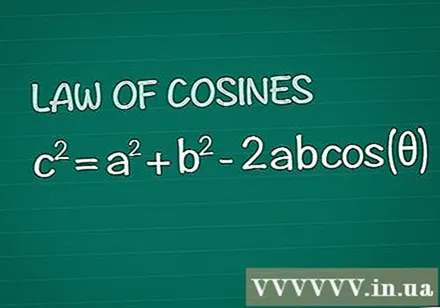

3. 

   Savienojiet divus vektorus, veidojot trīsstūri. Uzzīmējiet uz papīra divdimensiju vektoru pāri, vektorus un vektorus, θ ir leņķis starp tiem. Lai izveidotu trīsstūri, starp šiem diviem uzzīmējiet trešo vektoru. Citiem vārdiem sakot, uzzīmējiet vektoru tā, lai + =. Vektors = -.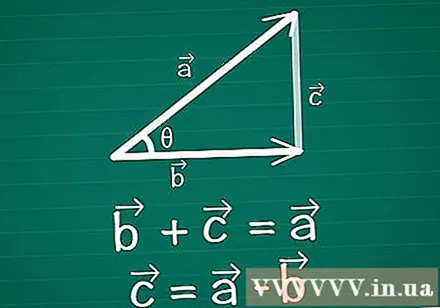

4. 

   Uzrakstiet šim trīsstūrim kosinusa teorēmu. Aizstājiet mūsu "vektora trīsstūra" sānu garumu Kosinusa teorēmā:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Pārrakstiet ar skalāru reizinājumu. Atcerieties, ka skalārais reizinājums ir viena vektora attēls. Vektora skalārajam produktam ar sevi nav nepieciešama projekcija, jo šeit nav atšķirības virzienā. Tas nozīmē, ka • = || a ||. Izmantojot to, mēs pārrakstām vienādojumu:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Veiksmīgi pārrakstīja to pašu formulu. Izvērsiet formulas kreiso pusi, pēc tam vienkāršojiet, lai iegūtu formulu, kas izmantota leņķu atrašanai.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   reklāma

Padoms

• Lai mainītu vērtības un ātri atrisinātu problēmu, izmantojiet šo formulu jebkuram divdimensiju vektoru pārim: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Ja strādājat ar datorgrafikas programmatūru, iespējams, jums būs jārūpējas tikai par vektoru dimensiju, neuztraucoties par to garumu. Veiciet šādas darbības, lai saīsinātu vienādojumu un paātrinātu programmu:
  • Normalizējiet katru vektoru tā, lai tie būtu vienādi ar 1. Lai to izdarītu, sadaliet katru no vektora komponentiem pēc tā garuma.
  • Iegūstiet skalāra normalizēto produktu sākotnējā vektora vietā.
  • Tā kā garums ir 1, mēs varam izslēgt garuma elementus no vienādojuma. Visbeidzot, iegūtais leņķa vienādojums ir arccos (•).
• Pamatojoties uz kosinusa formulu, mēs varam ātri noteikt, vai leņķis ir akūts vai neass. Sāciet ar cosθ = (•) / (|||| ||||):
  • Kreisajā un labajā vienādojuma pusē jābūt vienādai zīmei (pozitīvai vai negatīvai).
  • Tā kā garums vienmēr ir pozitīvs, cosθ jābūt ar tādu pašu zīmi kā skalārajam reizinājumam.
  • Tāpēc, ja produkts ir pozitīvs, arī cosθ ir pozitīvs. Mēs atrodamies vienības apļa pirmajā kvadrantā ar θ <π / 2 vai 90 °. Atrodamais leņķis ir asais leņķis.
  • Ja skalārais rezultāts ir negatīvs, cosθ ir negatīvs. Mēs atrodamies vienības apļa otrajā kvadrantā ar π / 2 <θ ≤ π vai 90º <θ ≤ 180º. Tas ir cietuma stūris.