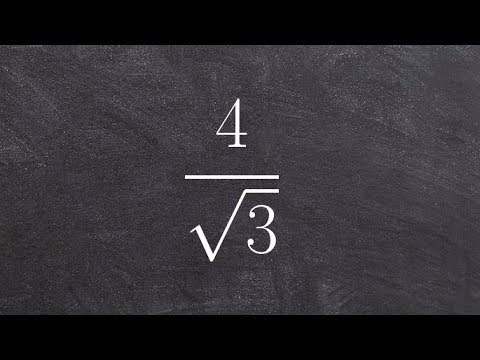
Saturs

• Soļi
• 1. metode no 4: Monomāls saucējā
• 2. metode no 4: Binomiāls saucējā
• 3. metode no 4: apgrieztā izteiksme
• 4. metode no 4: kubiskā saknes saucējs

Matemātikā nav pieņemts atstāt sakni vai neracionālu skaitli daļskaitlī. Ja saucējs ir sakne, reiziniet daļu ar kādu terminu vai izteiksmi, lai atbrīvotos no saknes. Mūsdienu kalkulatori ļauj strādāt ar saknēm saucējā, bet izglītības programma paredz, ka skolēniem jāspēj atbrīvoties no iracionalitātes saucējā.

Soļi

1. metode no 4: Monomāls saucējā

1. 1 Uzziniet daļu. Daļa tiek uzrakstīta pareizi, ja saucējā nav saknes. Ja saucējam ir kvadrāts vai kāda cita sakne, lai atbrīvotos no saknes, skaitītājs un saucējs jāreizina ar kādu monomu. Lūdzu, ņemiet vērā, ka skaitītājā var būt sakne - tas ir normāli.
   • ${ displaystyle { frac {7 { sqrt {3}}} {2 { sqrt {7}}}}}$
   • Saucējam šeit ir sakne ${ displaystyle { sqrt {7}}}$.
2. 2 Reiziniet skaitītāju un saucēju ar saucēja sakni. Ja saucējā ir monomāls, šādu daļu ir diezgan viegli racionalizēt. Reiziniet skaitītāju un saucēju ar vienu un to pašu monomu (tas ir, reiziniet daļu ar 1).
   • ${ displaystyle { frac {7 { sqrt {3}}} {2 { sqrt {7}}}} cdot { frac { sqrt {7}} { sqrt {7}}}}$
   • Ja kalkulatorā ievadāt risinājuma izteiksmi, noteikti ievietojiet iekavas ap katru daļu, lai tās atdalītu.
3. 3 Vienkāršojiet daļu (ja iespējams). Mūsu piemērā to var saīsināt, dalot skaitītāju un saucēju ar 7.
   • ${ displaystyle { frac {7 { sqrt {3}}} {2 { sqrt {7}}}} cdot { frac { sqrt {7}} { sqrt {7}}} = { frac {7 { sqrt {21}}} {14}} = { frac { sqrt {21}} {2}}}$

2. metode no 4: Binomiāls saucējā

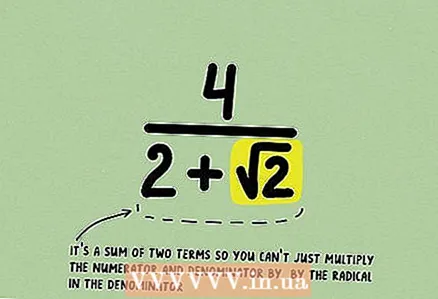1. 1 Uzziniet daļu. Ja tā saucējā ir divu monomālu summa vai starpība, no kuriem vienā ir sakne, nav iespējams reizināt daļu ar šādu binomiālu, lai atbrīvotos no iracionalitātes.
   • ${ displaystyle { frac {4} {2 + { sqrt {2}}}}}$
   • Lai to saprastu, pierakstiet daļu ${ displaystyle { frac {1} {a + b}}}$kur monomāls ${ displaystyle a}$ vai ${ displaystyle b}$ satur sakni. Šajā gadījumā: ${ displaystyle (a + b) (a + b) = a ^ {2} + 2ab + b ^ {2}}$... Tādējādi monomāls ${ displaystyle 2ab}$ joprojām ietvers sakni (ja ${ displaystyle a}$ vai ${ displaystyle b}$ satur sakni).
   • Apskatīsim mūsu piemēru.
     • ${ displaystyle { frac {4} {2 + { sqrt {2}}}} cdot { frac {2 + { sqrt {2}}} {2 + { sqrt {2}}}} = { frac {4 (2 + { sqrt {2}})} {4 + 4 { sqrt {2}} + 2}}}$
   • Jūs redzat, ka jūs nevarat atbrīvoties no monomāla saucējā ${ displaystyle 4 { sqrt {2}}}$.
2. 2 Reiziniet skaitītāju un saucēju ar binomiālā konjugātu saucējā. Konjugēts binoms ir binomiāls ar tādu pašu monomiju, bet starp tiem ir pretēja zīme. Piemēram, binom ${ displaystyle 2 + { sqrt {2}}}$ konjugēts ar binomiālu ${ displaystyle 2 - { sqrt {2}}.}$
   • ${ displaystyle { frac {4} {2 + { sqrt {2}}}} cdot { frac {2 - { sqrt {2}}} {2 - { sqrt {2}}}}}$
   • Izprotiet šīs metodes nozīmi. Vēlreiz apsveriet daļu ${ displaystyle { frac {1} {a + b}}}$... Reiziniet skaitītāju un saucēju ar binomālo konjugātu ar saucēja binomiālo: ${ displaystyle (a + b) (a -b) = a ^ {2} -b ^ {2}}$... Tādējādi nav monomiju, kas satur saknes. Tā kā monomi ${ displaystyle a}$ un ${ displaystyle b}$ ir kvadrātā, saknes tiks likvidētas.
3. 3 Vienkāršojiet daļu (ja iespējams). Ja gan skaitītājā, gan saucējā ir kāds kopīgs faktors, atceliet to. Mūsu gadījumā 4 - 2 = 2, ko var izmantot, lai samazinātu daļu.
   • ${ displaystyle { frac {4} {2 + { sqrt {2}}}} cdot { frac {2 - { sqrt {2}}} {2 - { sqrt {2}}}} = { frac {4 (2-{ sqrt {2}})} {4-2}} = 4-2 { sqrt {2}}}$

3. metode no 4: apgrieztā izteiksme

1. 1 Izpētiet problēmu. Ja jums jāatrod izteiksme, kas ir apgriezta dotajai, kurā ir sakne, jums būs racionalizēt iegūto daļu (un tikai pēc tam to vienkāršot). Šajā gadījumā izmantojiet pirmajā vai otrajā sadaļā aprakstīto metodi (atkarībā no uzdevuma).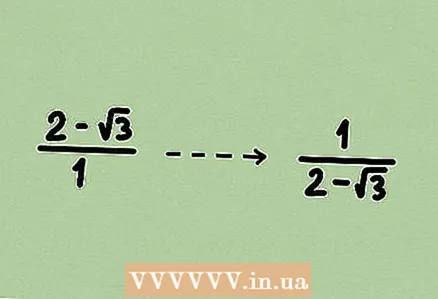
   • ${ displaystyle 2 - { sqrt {3}}}$
2. 2 Pierakstiet pretējo izteicienu. Lai to izdarītu, daliet 1 ar doto izteiksmi; ja ir dota daļiņa, nomainiet skaitītāju un saucēju. Atcerieties, ka jebkura izteiksme ir daļiņa ar 1 saucējā.
   • ${ displaystyle { frac {1} {2 - { sqrt {3}}}}}$
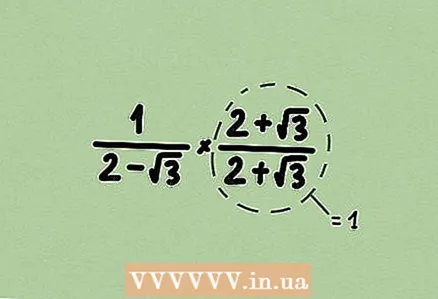3. 3 Reiziniet skaitītāju un saucēju ar kādu izteiksmi, lai atbrīvotos no saknes. Reizinot skaitītāju un saucēju ar vienu un to pašu izteiksmi, jūs reizināt daļu ar 1, tas ir, daļas vērtība nemainās. Mūsu piemērā mums ir dots binomiāls, tāpēc reiziniet skaitītāju un saucēju ar konjugēto binomiālu.
   • ${ displaystyle { frac {1} {2 - { sqrt {3}}}} cdot { frac {2 + { sqrt {3}}} {2 + { sqrt {3}}}}}$
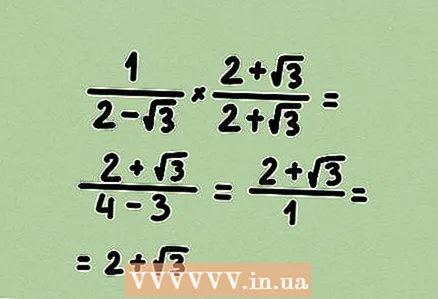4. 4 Vienkāršojiet daļu (ja iespējams). Mūsu piemērā 4 - 3 = 1, tāpēc izteiksmi frakcijas saucējā var pilnībā atcelt.
   • ${ displaystyle { frac {1} {2 - { sqrt {3}}}} cdot { frac {2 + { sqrt {3}}} {2 + { sqrt {3}}}} = { frac {2 + { sqrt {3}}} {4-3}} = 2 + { sqrt {3}}}$
   • Atbilde ir binomāls konjugāts ar šo binomiālo. Tā ir tikai sakritība.

4. metode no 4: kubiskā saknes saucējs

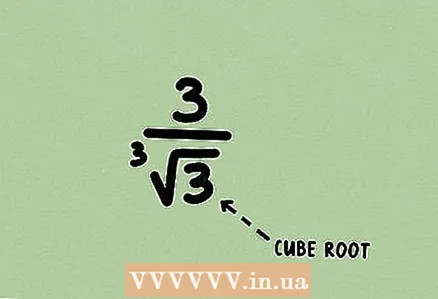1. 1 Uzziniet daļu. Problēma var saturēt kuba saknes, lai gan tas ir diezgan reti. Aprakstītā metode ir piemērojama jebkuras pakāpes saknēm.
   • ${ displaystyle { frac {3} { sqrt [{3}] {3}}}}$
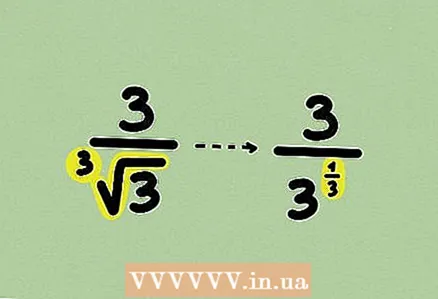2. 2 Pārrakstiet sakni kā spēku. Šeit jūs nevarat reizināt skaitītāju un saucēju ar kādu monomu vai izteiksmi, jo racionalizācija tiek veikta nedaudz savādāk.
   • ${ displaystyle { frac {3} {3 ^ {1/3}}}}$
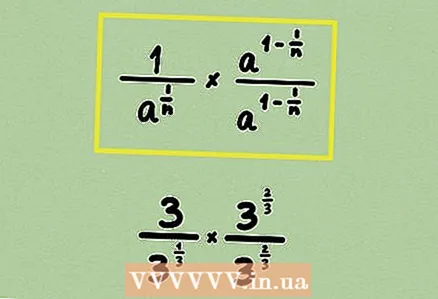3. 3 Reiziniet daļiņas skaitītāju un saucēju ar kādu jaudu, lai saucēja eksponents kļūtu par 1. Mūsu piemērā reiziniet daļu ar ${ displaystyle { frac {3 ^ {2/3}} {3 ^ {2/3}}}}$... Atcerieties, ka, reizinot grādus, to rādītāji sasummējas: ${ displaystyle a ^ {b} a ^ {c} = a ^ {b + c}.}$
   • ${ displaystyle { frac {3} {3 ^ {1/3}}} cdot { frac {3 ^ {2/3}} {3 ^ {2/3}}}}$
   • Šī metode ir piemērojama visām n pakāpes saknēm. Ja ir dota daļa ${ displaystyle { frac {1} {a ^ {1 / n}}}}$, reiziniet skaitītāju un saucēju ar ${ displaystyle a ^ {1 - { frac {1} {n}}}}$... Tādējādi saucēja eksponents kļūst par 1.
4. 4 Vienkāršojiet daļu (ja iespējams).
   • ${ displaystyle { frac {3} {3 ^ {1/3}}} cdot { frac {3 ^ {2/3}} {3 ^ {2/3}}} = 3 ^ {2/3 }}$
   • Ja nepieciešams, atbildē pierakstiet sakni. Mūsu piemērā eksponentu iedala divos faktoros: ${ displaystyle 1/3}$ un ${ displaystyle 2}$.
     • ${ displaystyle 3 ^ {2/3} = (3 ^ {2}) ^ {1/3} = { sqrt [{3}] {9}}}$