Saturs

• Lai soli
• 1. metode no 2: Pirmā metode: krustojuma reizināšana
• 2. metode no 2: Otrā metode: Vismazāko kopsaucēju (LCM) atrašana no saucējiem
• Padomi

Racionāla funkcija ir daļa ar vienu vai vairākiem mainīgajiem skaitītājā vai saucējā. Racionāls vienādojums ir jebkurš vienādojums, kas satur vismaz vienu racionālu izteicienu. Tāpat kā parastos algebriskos vienādojumus, arī racionālās izteiksmes var atrisināt, piemērojot to pašu darbību vienādojuma abām pusēm, līdz mainīgais tiek izolēts vienādības zīmes vienā pusē. Divas īpašas metodes, krusteniskā reizināšana un vismazāk sastopamā saucēju atkārtošanas atrašana, ir īpaši noderīgas mainīgo lielumu izolēšanai un racionālu vienādojumu risināšanai.

Lai soli

1. metode no 2: Pirmā metode: krustojuma reizināšana

1. Ja nepieciešams, pārkārtojiet vienādojumu, lai pārliecinātos, ka vienādības zīmes abās pusēs ir daļa. Krustu reizināšana ir ātra metode racionālu vienādojumu risināšanai. Diemžēl šī metode darbojas tikai racionāliem vienādojumiem, kuriem abās vienādības zīmes pusēs ir tieši viena racionāla izteiksme vai frakcija. Ja tas nav jūsu vienādojuma gadījums, jums, iespējams, ir nepieciešamas dažas algebriskas darbības, lai termini nonāktu pareizajā vietā.
   • Piemēram, vienādojumu (x + 3) / 4 - x / (- 2) = 0 var viegli pārvērst pareizajā krustojuma reizināšanas formā, pievienojot x / (- 2) vienādojuma abām pusēm, padarot to rezultātu izskatās šādi: (x + 3) / 4 = x / (- 2).
     • Atcerieties, ka decimāldaļas un veselos skaitļus var pārvērst daļās, dodot viņiem saucēju 1. Piemēram, (x + 3) / 4 - 2,5 = 5, var pārrakstīt kā (x + 3) / 4 = 7,5 / 1, kas ļauj piemērot krustenisko reizināšanu.
   • Dažus racionālus vienādojumus nevar viegli pārveidot pareizajā formā. Šādos gadījumos izmantojiet metodes, kurās izmantojat vismazāk sastopamo saucēju daudzkārtni.
2. Krustu reizināšana. Krusteniskā reizināšana vienkārši nozīmē vienas daļas skaitītāja reizināšanu ar otras daļas saucēju un otrādi. Reiziniet frakcijas skaitītāju pa kreisi no vienādības zīmes ar labās puses daļu. Atkārtojiet ar skaitītāju labajā pusē un frakcijas saucēju pa kreisi.
   • Krustu reizināšana darbojas pēc kopīgiem algebriskiem principiem. Racionālās izteiksmes un citas daļas var pārvērst parastajos skaitļos, reizinot saucējus. Būtībā krusteniskā reizināšana ir ērts stenogrāfisks veids, kā reizināt abas vienādojuma puses ar abiem frakciju saucējiem. Vai jūs tam neticat? Izmēģiniet - pēc vienkāršošanas redzēsit tos pašus rezultātus.
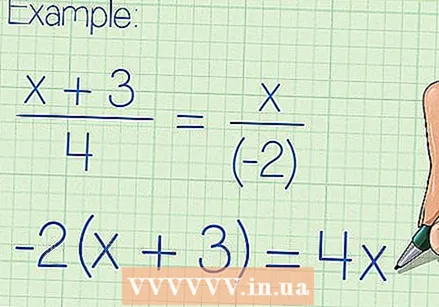3. Padariet abus produktus vienādus. Pēc krustojuma reizināšanas jums paliek divi produkti. Padariet šos divus vienādus un vienkāršojiet tos, lai iegūtu vienkāršākos vienādojumus abās vienādojuma pusēs.
   • Piemēram, ja (x + 3) / 4 = x / (- 2) bija jūsu sākotnējā racionālā izteiksme, tad pēc krustojuma reizināšanas tā kļūst vienāda ar -2 (x + 3) = 4x. Pēc izvēles to var pārrakstīt kā -2x - 6 = 4x.
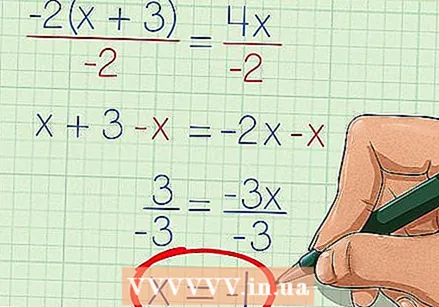4. Atrisiniet mainīgo. Izmantojiet algebras darbības, lai vienādojumā atrastu mainīgā lielumu. Atcerieties, ja x parādās vienādības zīmes abās pusēs, tad, saskaitot vai atņemot x terminu, pārliecinieties, ka vienādības zīmes vienā pusē ir tikai x termini.
   • Mūsu piemērā ir iespējams sadalīt abas vienādojuma puses ar -2, kas dod mums x + 3 = -2x. Atņemot x no vienādības zīmes abām pusēm, iegūstam 3 = -3x. Un visbeidzot, dalot abas puses ar -3, iegūstam -1 = x, vai arī x = -1. Tagad mēs esam atraduši x, kas atrisina mūsu racionālo vienādojumu.

2. metode no 2: Otrā metode: Vismazāko kopsaucēju (LCM) atrašana no saucējiem

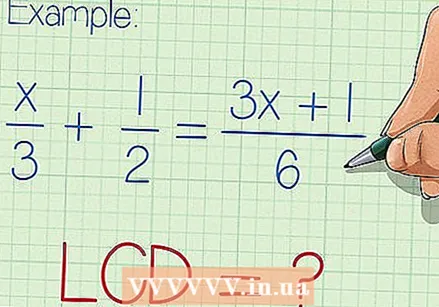1. Saprotiet, kad ir acīmredzami atrast vismazāk sastopamo saucēju daudzkārtni. Vismazāko kopsaucēju (LCM) no saucējiem var izmantot, vienkāršojot racionālos vienādojumus, ļaujot atrast to mainīgo lielumus. LCM atrašana ir laba ideja, ja racionālo vienādojumu nevar viegli pārrakstīt formā, kur vienādības zīmes katrā pusē ir tikai viena daļa vai racionāla izteiksme. Racionālu vienādojumu risināšanai ar trim vai vairākiem termiņiem LCM ir noderīgs rīks. Bet, lai atrisinātu racionālus vienādojumus tikai ar diviem terminiem, krustu reizināšana bieži notiek ātrāk.
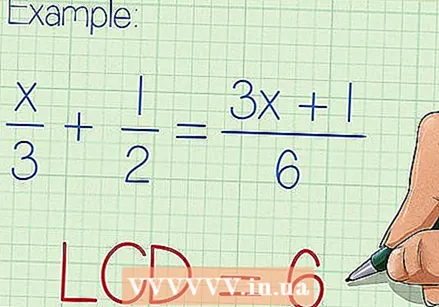2. Pārbaudiet katras frakcijas saucēju. Atrodiet mazāko skaitli, kas ir pilnīgi dalāms ar jebkuru saucēju. Tas ir jūsu vienādojuma LCM.
   • Dažreiz uzreiz redzams vismazāk izplatītais daudzkārtnis - mazākais skaitlis, kas ir pilnīgi dalāms ar katru saucēju. Piemēram, ja jūsu izteiksme izskatās kā x / 3 + 1/2 = (3x + 1) / 6, tad ir viegli saprast, ka LCM jābūt dalāmam ar 3, 2 un 6 un tādējādi vienādam ar 6.
   • Bet biežāk racionāla salīdzinājuma LCM nemaz nav uzreiz skaidrs. Tādos gadījumos izmēģiniet lielākā saucēja reizinātājus, līdz atrodat skaitli, kurā iekļauti citu, mazāku saucēju daudzkārtņi. Bieži vien LCM ir divu saucēju reizinājums. Piemēram, ņem vienādojumu x / 8 + 2/6 = (x - 3) / 9, kur LCM ir vienāds ar 8 * 9 = 72.
   • Ja vienā vai vairākos saucējos ir mainīgais, šis process būs nedaudz grūtāks, taču tas nebūt nav neiespējams. Šajos gadījumos LCM ir izteiksme (ar mainīgajiem), kas pilnībā atbilst visiem saucējiem, ne tikai vienam skaitlim. Piemēram, vienādojums 5 / (x-1) = 1 / x + 2 / (3x), kur LCM ir vienāds ar 3x (x-1), jo tas ir pilnīgi dalāms ar jebkuru saucēju - dalījums ar (x- 1 ) dod 3x, dalot ar 3x ražu (x-1) un dalot ar x, iegūst 3 (x-1).
3. Katru daļu racionālajā vienādojumā reiziniet ar 1. Katra vārda reizināšana ar 1 var šķist bezjēdzīga, taču šeit ir kāds triks. Proti, 1 var rakstīt kā daļu - piemēram, 2/2 un 3/3. Reiziniet katru sava racionālā vienādojuma daļu ar 1, katru reizi ierakstot 1 kā skaitli vai terminu, kas reizināts ar katru saucēju, lai iegūtu LCM kā daļu.
   • Mūsu piemērā mēs varam reizināt x / 3 ar 2/2, lai iegūtu 2x / 6, un reizināt 1/2 ar 3/3, lai iegūtu 3/6. 3x +1/6 jau ir 6 (lcm) saucējs, tāpēc mēs varam to reizināt ar 1/1 vai vienkārši atstāt.
   • Mūsu piemērā ar mainīgajiem skaitļos viss process ir nedaudz sarežģītāks. Tā kā LCM ir vienāds ar 3x (x-1), katru racionālo izteiksmi reizinām ar daļu, kas kā saucēju dod 3x (x-1). Mēs reizinām 5 / (x-1) ar (3x) / (3x), un tas dod 5 (3x) / (3x) (x-1), reizinām 1 / x ar 3 (x-1) / 3 (x -1), un tas dod 3 (x-1) / 3x (x-1), un mēs reizinām 2 / (3x) ar (x-1) / (x-1), un tas beidzot dod 2 (x-1) / 3x (x-1).
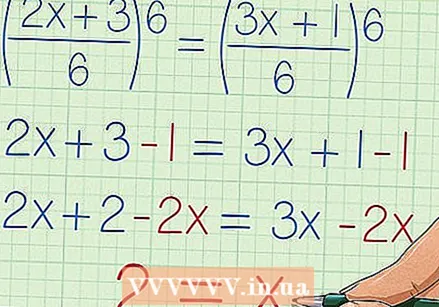4. Vienkāršojiet un atrisiniet x. Tagad, kad katram jūsu racionālā vienādojuma terminam ir viens un tas pats saucējs, ir iespējams izslēgt saucējus no vienādojuma un atrisināt skaitītājus. Vienkārši reiziniet abas vienādojuma puses ar LCM, lai atbrīvotos no saucējiem, lai jums paliktu tikai skaitītāji. Tagad tas ir kļuvis par regulāru vienādojumu, kuru jūs varat atrisināt mainīgajam, izolējot to vienādības zīmes vienā pusē.
   • Mūsu piemērā pēc reizināšanas, lietojot 1 kā daļu, iegūstam 2x / 6 + 3/6 = (3x + 1) / 6. Divas frakcijas var pievienot, ja tām ir viens un tas pats saucējs, tāpēc mēs varam uzrakstīt šo vienādojumu kā (2x + 3) / 6 = (3x + 1) / 6, nemainot tā vērtību. Reiziniet abas puses ar 6, lai atceltu saucējus, atstājot 2x + 3 = 3x + 1. Šeit atņemiet 1 no abām pusēm, lai atstātu 2x + 2 = 3x, un atņemiet 2x no abām pusēm, lai atstātu 2 = x, ko pēc tam var ierakstīt arī kā x = 2.
   • Mūsu piemērā ar mainīgajiem saucējos vienādojums pēc katra termina reizināšanas ar "1" ir vienāds ar 5 (3x) / (3x) (x-1) = 3 (x-1) / 3x (x-1) + 2 ( x-1) / 3x (x-1). Reizinot katru terminu ar LCM, ir iespējams atcelt saucējus, kas tagad dod mums 5 (3x) = 3 (x-1) + 2 (x-1). Izstrādājot tālāk, tas kļūst par 15x = 3x - 3 + 2x -2, ko atkal var vienkāršot kā 15x = x - 5. Atņemot x no abām pusēm, iegūst 14x = -5, lai galīgo atbildi varētu vienkāršot līdz x = - 5/14.

Padomi

• Kad esat atradis mainīgā vērtību, pārbaudiet atbildi, ievadot šo vērtību sākotnējā vienādojumā. Ja iegūstat mainīgā lieluma vērtību pareizi, jums vajadzētu būt iespējai vienkāršot vienādojumu ar vienkāršu, pareizu teorēmu, piemēram, 1 = 1.
• Katru vienādojumu var uzrakstīt kā racionālu izteicienu; vienkārši novietojiet to kā skaitītāju virs saucēja 1. Tātad vienādojumu x + 3 var uzrakstīt kā (x + 3) / 1, abiem ir vienāda vērtība.