Saturs

• Soļi
• Padomi

Racionālajai funkcijai ir forma y = N (x) / D (x), kur N un D ir polinomi. Lai precīzi uzzīmētu šādu funkciju, jums ir nepieciešamas labas zināšanas par algebru, ieskaitot diferenciālos aprēķinus. Apsveriet šādu piemēru: y = (2x - 6x + 5)/(4x + 2).

Soļi

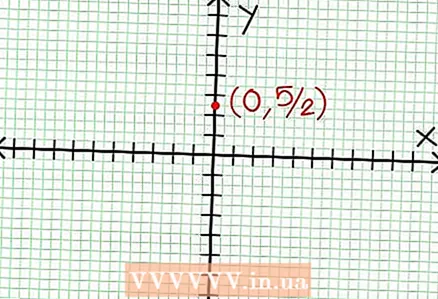1. 1 Atrodiet grafika y krustojumu. Lai to izdarītu, aizstājiet funkciju x = 0 un iegūstiet y = 5/2. Tādējādi grafika krustošanās punktam ar Y asi ir koordinātas (0, 5/2).Novietojiet šo punktu koordinātu plaknē.
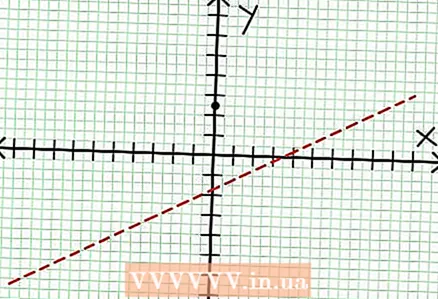2. 2 Atrodiet horizontālos asimptotus. Sadaliet skaitītāju ar saucēju (kolonnā), lai noteiktu "y" uzvedību ar "x" vērtībām, kas tiecas uz bezgalību. Mūsu piemērā sadalījums būs y = (1/2)x - (7/4) + 17/(8x + 4). Lielām pozitīvām vai negatīvām vērtībām "x" 17 / (8x + 4) ir tendence uz nulli, un grafiks tuvojas funkcijas dotajai taisnei y = (1/2)x - (7/4). Izmantojot punktēto līniju, uzzīmējiet šo funkciju.
   • Ja skaitītāja pakāpe ir mazāka par saucēja pakāpi, tad jūs nevarat dalīt skaitītāju ar saucēju, un asimptotu aprakstīs funkcija plkst = 0.
   • Ja skaitītāja pakāpe ir vienāda ar saucēja pakāpi, tad asimptote ir horizontāla līnija, kas vienāda ar koeficientu attiecību "x" augstākajā pakāpē.
   • Ja skaitītāja pakāpe ir par 1 lielāka nekā saucēja pakāpe, tad asimptote ir slīpa taisne, kuras slīpums ir vienāds ar koeficientu attiecību "x" augstākajā pakāpē.
   • Ja skaitītāja pakāpe ir lielāka par saucēja pakāpi par 2, 3 utt., Tad lielām vērtībām |NS| nozīme plkst tendence uz bezgalību (pozitīva vai negatīva) kvadrāta, kubiskā vai cita polinoma pakāpes formā. Šajā gadījumā, visticamāk, jums nav jāveido precīzs funkcijas grafiks, kas iegūts, dalot skaitītāju ar saucēju.
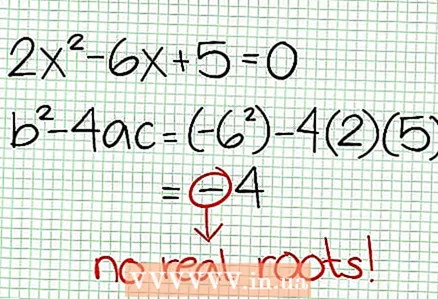3. 3 Atrodiet funkcijas nulles. Racionālai funkcijai ir nulles, ja tās skaitītājs ir nulle, tas ir, N (NS) = 0. Mūsu piemērā 2x - 6x + 5 = 0. Šī kvadrātiskā vienādojuma diskriminants: b - 4ac = 6 - 4 * 2 * 5 = 36 - 40 = -4. Tā kā diskriminants ir negatīvs, tad N (NS), un līdz ar to F (NS) nav īstu sakņu. Racionālas funkcijas grafiks nešķērso X asi.Ja funkcijai ir nulles (saknes), tad ievietojiet tās koordinātu plaknē.
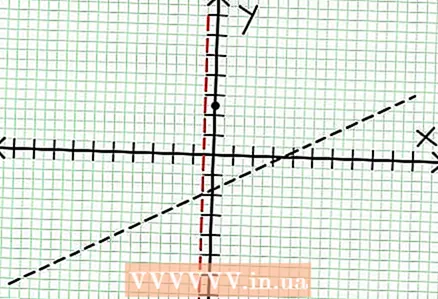4. 4 Atrodiet vertikālos asimptotus. Lai to izdarītu, iestatiet saucēju uz nulli. Mūsu piemērā 4x + 2 = 0 un NS = -1/2. Uzzīmējiet vertikālo asimptotu, izmantojot punktētu līniju. Ja par kādu vērtību NS N (NS) = 0 un D (NS) = 0, tad vertikālais asimptots vai nu pastāv, vai neeksistē (tas ir rets gadījums, bet labāk to atcerēties).
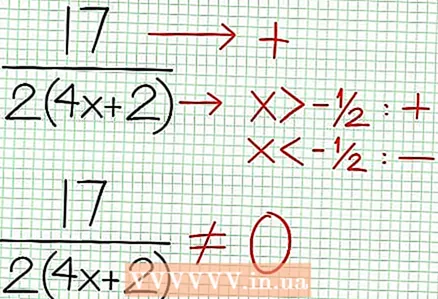5. 5 Apskatiet atlikušo skaitītāja daļu, kas dalīta ar saucēju. Vai tas ir pozitīvs, negatīvs vai nulle? Mūsu piemērā atlikums ir 17, kas ir pozitīvi. Saucējs 4x + 2 pozitīvi pa labi no vertikālā asimptota un negatīvi pa kreisi no tā. Tas nozīmē, ka racionālās funkcijas grafiks lielām pozitīvām vērtībām NS tuvojas asimptotam no augšas un lielām negatīvām vērtībām NS - no apakšas. Kopš 17 / (8x + 4) nekad nav vienāds ar nulli, tad šīs funkcijas grafiks nekad nekrustojas funkcijas norādīto taisni plkst = (1/2)NS - (7/4).
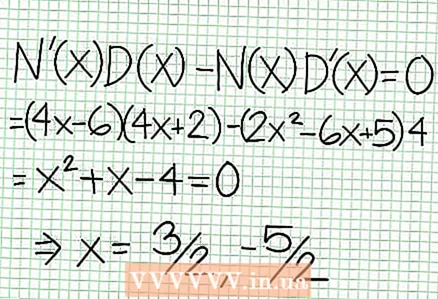6. 6 Atrodiet vietējo galējību. Pastāv vietēja ekstrēma N '(x) D (x) - N (x) D ’(x) = 0. Mūsu piemērā N ’(x) = 4x - 6 un D '(x) = 4. N ’(x) D (x) - N (x) D ’(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Atrisinot šo vienādojumu, jūs atradīsit, ka x = 3/2 un x = -5/2. (Šīs nav pilnīgi precīzas vērtības, taču tās ir piemērotas mūsu gadījumam, kad nav nepieciešama precīza precizitāte.)
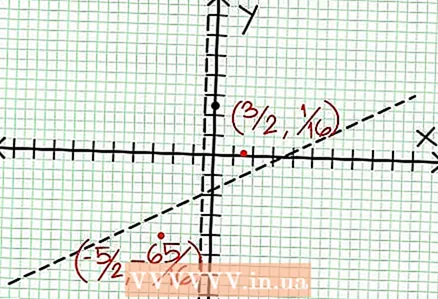7. 7 Atrodiet vērtību plkst par katru vietējo ekstrēmumu. Lai to izdarītu, aizstājiet vērtības NS sākotnējā racionālajā funkcijā. Mūsu piemērā f (3/2) = 1/16 un f (-5/2) = -65/16. Atlieciet koordinātu plaknē punktus (3/2, 1/16) un (-5/2, -65/16). Tā kā aprēķini ir balstīti uz aptuvenām vērtībām (no iepriekšējā soļa), atrastie minimālie un maksimālie arī nav pilnīgi precīzi (bet, iespējams, ļoti tuvu precīzām vērtībām). (Punkts (3/2, 1/16) ir ļoti tuvu vietējam minimumam. Sākot no 3. soļa, mēs to zinām plkst vienmēr pozitīvi par NS> -1/2, un mēs atradām nelielu vērtību (1/16); tādējādi kļūdas vērtība šajā gadījumā ir ārkārtīgi maza.)
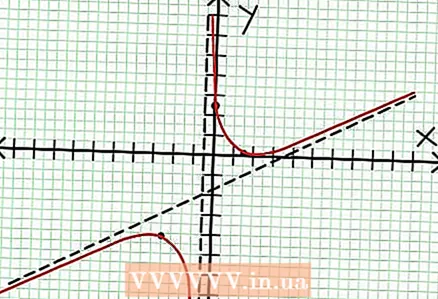8. 8 Savienojiet gaidāmos punktus un vienmērīgi pagariniet grafiku līdz asimptotēm (neaizmirstiet par pareizo grafika virzienu, kas tuvojas asimptotēm). Atcerieties, ka grafiks nedrīkst šķērsot X asi (skat. 3. darbību). Diagramma arī nekrustojas ar horizontālajiem un vertikālajiem asimptotiem (skat. 5. soli). Nemainiet diagrammas virzienu, izņemot iepriekšējā solī atrastos galējos punktus.

Padomi

• Ja jūs stingri ievērojāt iepriekš minētās darbības, jums nav jāaprēķina otrie atvasinājumi (vai līdzīgi sarežģīti daudzumi), lai pārbaudītu risinājumu.
• Ja jums nav jāaprēķina lielumu vērtības, vietējo galējību atrašanu var aizstāt, aprēķinot dažus papildu koordinātu pārus (NS, plkst) starp katru asimptotu pāri. Turklāt, ja jums vienalga, kā aprakstītā metode darbojas, nebrīnieties, kāpēc nevarat atrast atvasinājumu un atrisināt vienādojumu N '(x) D (x) - N (x) D ’(x) = 0.
• Dažos gadījumos jums būs jāstrādā ar augstākas kārtas polinomiem. Ja nevarat atrast precīzu risinājumu, izmantojot faktorizāciju, formulas utt., Novērtējiet iespējamos risinājumus, izmantojot skaitliskas metodes, piemēram, Ņūtona metodi.
• Retos gadījumos skaitītājam un saucējam ir kopīgs mainīgais koeficients. Saskaņā ar aprakstītajām darbībām tas novedīs pie nulles un vertikāla asimptota tajā pašā vietā. Tomēr tas nav iespējams, un skaidrojums ir viens no šiem:
  • Nulle n (NS) ir lielāks reizinājums nekā nulle D (NS). F diagramma (NS) šajā brīdī mēdz būt nulle, bet tur nav definēts. Norādiet to, uzzīmējot apli ap punktu.
  • Nulle n (NS) un nulle D (NS) ir vienāds daudzkārtīgums. Grafiks pie šīs vērtības tuvojas kādam punktam, kas nav nulle NSbet tur nav definēts. Norādiet to, uzzīmējot apli ap punktu.
  • Nulle n (NS) ir mazāks reizinājums nekā nulle D (NS). Šeit ir vertikāls asimptots.