Saturs

• Soļi
• 1. metode no 3: kā atrisināt kubisko vienādojumu bez nemainīga termiņa
• 2. metode no 3: kā atrast veselas saknes, izmantojot reizinātājus
• 3. metode no 3: kā atrisināt vienādojumu, izmantojot diskriminantu

Kubiskajā vienādojumā augstākais eksponents ir 3, šādam vienādojumam ir 3 saknes (risinājumi) un tam ir forma ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Dažus kubikvienādojumus nav tik viegli atrisināt, taču, ja izmantojat pareizo metodi (ar labu teorētisko pamatojumu), varat atrast pat vissarežģītākā kubiskā vienādojuma saknes - šim nolūkam izmantojiet kvadrātvienādojuma atrisināšanas formulu. veselas saknes, vai aprēķināt diskriminantu.

Soļi

1. metode no 3: kā atrisināt kubisko vienādojumu bez nemainīga termiņa

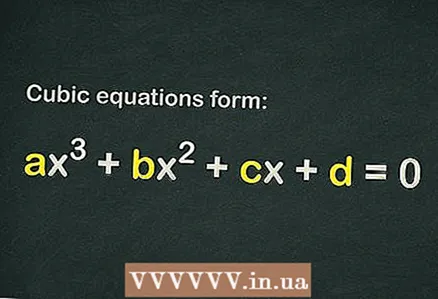1. 1 Uzziniet, vai kubiskā vienādojumā ir brīvs termins d{ displaystyle d}. Kubiskajam vienādojumam ir forma ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Lai vienādojumu uzskatītu par kubikmetru, pietiek tikai ar terminu ${ displaystyle x ^ {3}}$ (tas ir, citu dalībnieku vispār var nebūt).
   • Ja vienādojumam ir brīvs termins ${ displaystyle d}$, izmantojiet citu metodi.
   • Ja vienādojumā ${ displaystyle a = 0}$, tas nav kub.
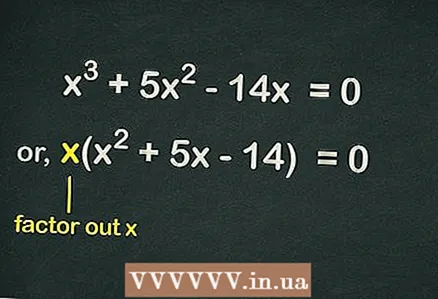2. 2 Izņemiet no iekavām x{ displaystyle x}. Tā kā vienādojumā nav brīva termina, katrs vienādojuma termins ietver mainīgo ${ displaystyle x}$... Tas nozīmē, ka viens ${ displaystyle x}$ var izslēgt no iekavām, lai vienkāršotu vienādojumu. Tādējādi vienādojums tiks uzrakstīts šādi: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • Piemēram, ņemot vērā kubisko vienādojumu ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Izņemt ${ displaystyle x}$ iekavās un saņemt ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
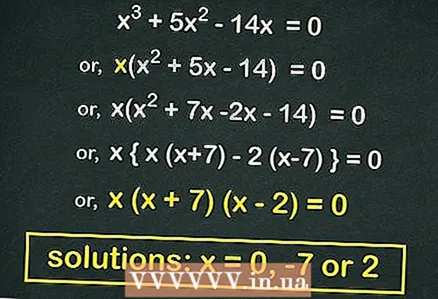3. 3 Faktors (divu binomiālu reizinājums) kvadrātvienādojums (ja iespējams). Daudzi formas kvadrātvienādojumi ${ displaystyle ax ^ {2} + bx + c = 0}$ var faktorizēt. Šāds vienādojums izrādīsies, ja mēs izņemsim ${ displaystyle x}$ ārpus iekavām. Mūsu piemērā:
   • Izņemiet no iekavām ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Faktors kvadrātvienādojums: ${ displaystyle x (x + 7) (x-2) = 0}$
   • Katru tvertni pielīdziniet ${ displaystyle 0}$... Šī vienādojuma saknes ir ${ displaystyle x = 0, x = -7, x = 2}$.
4. 4 Atrisiniet kvadrātvienādojumu, izmantojot īpašu formulu. Dariet to, ja kvadrātvienādojumu nevar faktorizēt. Lai atrastu divas vienādojuma saknes, koeficientu vērtības ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ aizstājējs formulā ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • Mūsu piemērā aizstājiet koeficientu vērtības ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ displaystyle -2}$, ${ displaystyle 14}$) formulā:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Pirmā sakne:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • Otrā sakne:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Izmantojiet nulles un kvadrātiskās saknes kā kubiskā vienādojuma risinājumus. Kvadrātvienādojumiem ir divas saknes, bet kubiskajiem - trīs. Jūs jau esat atradis divus risinājumus - tās ir kvadrātvienādojuma saknes. Ja jūs ievietojat "x" ārpus iekavām, trešais risinājums būtu ${ displaystyle 0}$.
   • Ja izņemat "x" no iekavām, jūs saņemsiet ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, tas ir, divi faktori: ${ displaystyle x}$ un kvadrātvienādojums iekavās. Ja kāds no šiem faktoriem ir ${ displaystyle 0}$, arī viss vienādojums ir vienāds ar ${ displaystyle 0}$.
   • Tādējādi divas kvadrātvienādojuma saknes ir kubiskā vienādojuma risinājumi. Trešais risinājums ir ${ displaystyle x = 0}$.

2. metode no 3: kā atrast veselas saknes, izmantojot reizinātājus

1. 1 Pārliecinieties, vai kubiskā vienādojumā ir brīvs termins d{ displaystyle d}. Ja formas vienādojumā ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ ir brīvs biedrs ${ displaystyle d}$ (kas nav vienāds ar nulli), nestrādās "x" ārpus iekavām. Šajā gadījumā izmantojiet šajā sadaļā izklāstīto metodi.
   • Piemēram, ņemot vērā kubisko vienādojumu ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Lai vienādojuma labajā pusē iegūtu nulli, pievienojiet ${ displaystyle 6}$ uz abām vienādojuma pusēm.
   • Vienādojums izrādīsies ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Kā ${ displaystyle d = 6}$, pirmajā sadaļā aprakstīto metodi nevar izmantot.
2. 2 Pierakstiet koeficienta faktorus a{ displaystyle a} un bezmaksas biedrs d{ displaystyle d}. Tas ir, atrodiet skaitļa faktorus pie ${ displaystyle x ^ {3}}$ un cipari pirms vienādības zīmes. Atgādiniet, ka skaitļa faktori ir skaitļi, kas, reizinot, rada šo skaitli.
   • Piemēram, lai iegūtu numuru 6, vajag pavairot ${ displaystyle 6 reizes 1}$ un ${ displaystyle 2 reizes 3}$... Tātad skaitļi 1, 2, 3, 6 ir skaitļa faktori 6.
   • Mūsu vienādojumā ${ displaystyle a = 2}$ un ${ displaystyle d = 6}$... Reizinātāji 2 ir 1 un 2... Reizinātāji 6 ir skaitļi 1, 2, 3 un 6.
3. 3 Sadaliet katru faktoru a{ displaystyle a} par katru faktoru d{ displaystyle d}. Tā rezultātā jūs saņemat daudz frakciju un vairākus veselus skaitļus; kubiskā vienādojuma saknes būs viens no veseliem skaitļiem vai viena no veseliem skaitļiem negatīvā vērtība.
   • Mūsu piemērā sadaliet faktorus ${ displaystyle a}$ (1 un 2) pēc faktoriem ${ displaystyle d}$ (1, 2, 3 un 6). Jūs saņemsiet: ${ displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ un ${ displaystyle { frac {2} {3}}}$... Tagad pievienojiet šim sarakstam iegūto frakciju un skaitļu negatīvās vērtības: ${ displaystyle 1}$, ${ displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ un ${ displaystyle - { frac {2} {3}}}$... Visas kubiskā vienādojuma saknes ir daži skaitļi no šī saraksta.
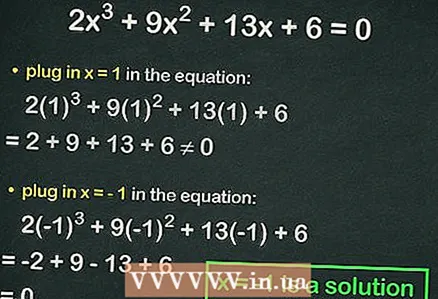4. 4 Pievienojiet kubikvienādojumam veselus skaitļus. Ja vienādība ir patiesa, aizvietotais skaitlis ir vienādojuma sakne. Piemēram, aizstāt vienādojumā ${ displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, tas ir, netiek ievērota vienlīdzība. Šādā gadījumā pievienojiet nākamo numuru.
   • Aizstājējs ${ displaystyle -1}$: ${ displeja stils (-2) +9 +(- 13) +6}$ = 0. Tādējādi, ${ displaystyle -1}$ ir visa vienādojuma sakne.
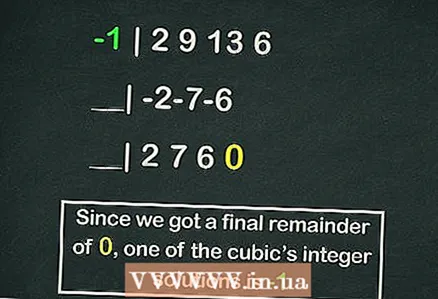5. 5 Izmantojiet polinomu dalīšanas metodi ar Hornera shēmalai ātrāk atrastu vienādojuma saknes. Dariet to, ja nevēlaties manuāli aizstāt skaitļus vienādojumā. Hornera shēmā veseli skaitļi tiek dalīti ar vienādojuma koeficientu vērtībām ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ un ${ displaystyle d}$... Ja skaitļi ir vienmērīgi dalāmi (tas ir, pārējais ir ${ displaystyle 0}$), vienādojuma sakne ir vesels skaitlis.
   • Hornera shēma ir pelnījusi atsevišķu rakstu, bet šāds ir piemērs, kā aprēķināt vienu no mūsu kubiskā vienādojuma saknēm, izmantojot šo shēmu:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Tātad atlikums ir ${ displaystyle 0}$, bet ${ displaystyle -1}$ ir viena no vienādojuma saknēm.

3. metode no 3: kā atrisināt vienādojumu, izmantojot diskriminantu

1. 1 Pierakstiet vienādojuma koeficientu vērtības a{ displaystyle a}, b{ displaystyle b}, c{ displaystyle c} un d{ displaystyle d}. Mēs iesakām iepriekš pierakstīt norādīto koeficientu vērtības, lai turpmāk neapjuktu.
   • Piemēram, ņemot vērā vienādojumu ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$... Pierakstīt ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ un ${ displaystyle d = -1}$... Atgādiniet, ka, ja agrāk ${ displaystyle x}$ nav skaitļa, atbilstošais koeficients joprojām pastāv un ir vienāds ar ${ displaystyle 1}$.
2. 2 Aprēķiniet nulles diskriminantu, izmantojot īpašu formulu. Lai atrisinātu kubisko vienādojumu, izmantojot diskriminantu, jums ir jāveic vairāki sarežģīti aprēķini, bet, ja visas darbības veicat pareizi, šī metode kļūs neaizstājama, lai atrisinātu vissarežģītākos kubikvienādojumus. Vispirms aprēķiniet ${ displaystyle Delta _ {0}}$ (nulles diskriminants) ir pirmā vērtība, kas mums nepieciešama; lai to izdarītu, aizstājiet atbilstošās vērtības formulā ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • Diskriminants ir skaitlis, kas raksturo polinoma saknes (piemēram, kvadrātvienādojuma diskriminantu aprēķina pēc formulas ${ displaystyle b ^ {2} -4ac}$).
   • Mūsu vienādojumā:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Aprēķiniet pirmo diskriminantu, izmantojot formulu Δ1=2b3−9abc+27a2d{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Pirmais diskriminants ${ displaystyle Delta _ {1}}$ - šī ir otrā nozīmīgā vērtība; lai to aprēķinātu, pievienojiet atbilstošās vērtības norādītajā formulā.
   • Mūsu vienādojumā:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Aprēķināt:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Tas ir, atrodiet kubiskā vienādojuma diskriminantu, izmantojot iegūtās vērtības ${ displaystyle Delta _ {0}}$ un ${ displaystyle Delta _ {1}}$... Ja kubiskā vienādojuma diskriminants ir pozitīvs, vienādojumam ir trīs saknes; ja diskriminants ir nulle, vienādojumam ir viena vai divas saknes; ja diskriminants ir negatīvs, vienādojumam ir viena sakne.
   • Kubikvienādojumam vienmēr ir vismaz viena sakne, jo šī vienādojuma grafiks krusto X asi vismaz vienā punktā.
   • Mūsu vienādojumā ${ displaystyle Delta _ {0}}$ un ${ displaystyle Delta _ {1}}$ ir vienlīdzīgi ${ displaystyle 0}$, lai jūs varētu viegli aprēķināt ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Tādējādi mūsu vienādojumam ir viena vai divas saknes.

5. 5 Aprēķināt:${ displaystyle C = ^ {3} { sqrt { pa kreisi ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } pa labi) div 2}}}$. ${ displaystyle C}$ - tas ir pēdējais svarīgais daudzums, kas jāatrod; tas palīdzēs aprēķināt vienādojuma saknes. Aizstājiet vērtības norādītajā formulā ${ displaystyle Delta _ {1}}$ un ${ displaystyle Delta _ {0}}$.
   • Mūsu vienādojumā:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 Atrodiet trīs vienādojuma saknes. Dariet to ar formulu ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, kur ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, bet n ir vienāds ar 1, 2 vai 3... Aizstājiet atbilstošās vērtības šajā formulā - rezultātā jūs iegūsit trīs vienādojuma saknes.
   • Aprēķiniet vērtību, izmantojot formulu pie n = 1, 2 vai 3un tad pārbaudiet atbildi. Ja, pārbaudot atbildi, saņemat 0, šī vērtība ir vienādojuma sakne.
   • Mūsu piemērā aizstājējs 1 iekšā ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$ un saņemties 0, t.i 1 ir viena no vienādojuma saknēm.